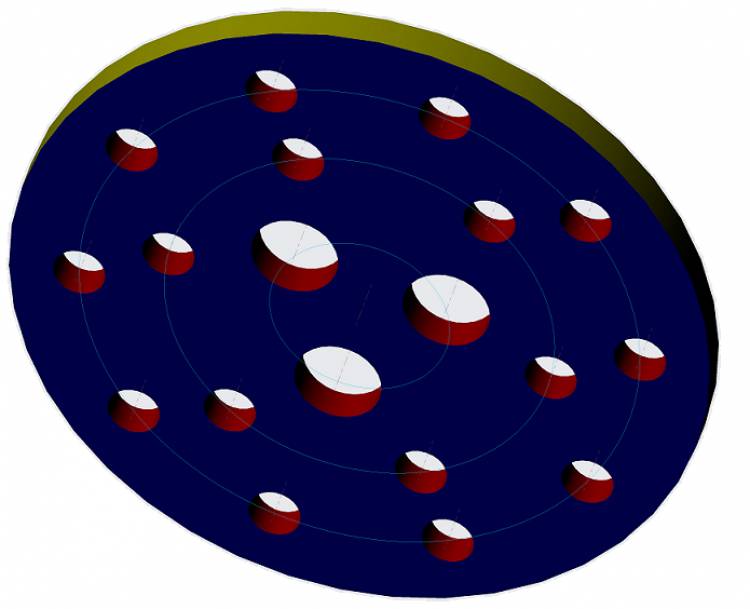
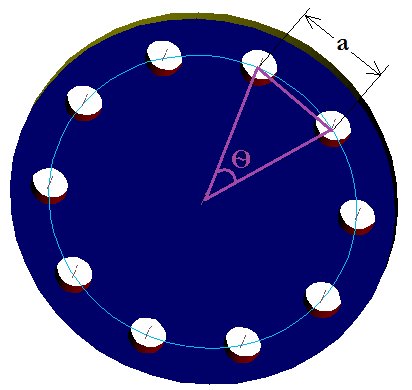
What is PCD? How to calculate the distance between the two adjacent holes?
PCD stands for pitch circle diameter. If there are certain number of holes are in a circle and divided equally then we say the diameter of the circle as pitch circle diameter. To calculate the division (distance between two nearby holes) of the PCD , multiply the diameter of the pitch circle and the given factor in the table. For instance, If 10 holes to be equally divided in a 100 mm pitch circle then the division, a = dia x 0.309 = 100 x 0.309 = 30.90 mm. You can find the table at the end of this article.
PCD:
PCD stands for pitch circle diameter. If there are certain number of holes are in a circle and divided equally then we say the diameter of the circle as pitch circle diameter.

How to calculate it?
It differs according to the number of holes in the circle.
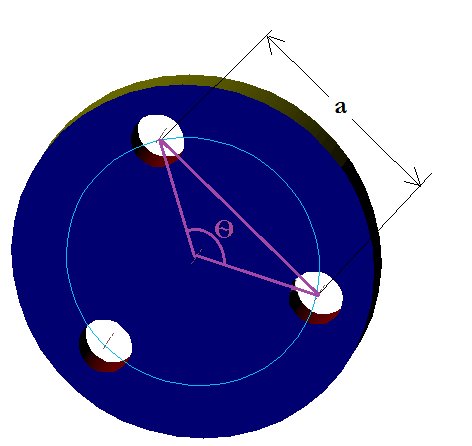
1.For three holes:


The total degree of the circle = 3600
If we form a triangle joining the centre of the circle and the centre of the two adjacent holes as shown in the figure,
We could see the adjacent sides of the triangle forms degree Ѳ and if we divide the triangle into two it forms a right angle triangle with Ѳ/2 degree.
Ѳ = 3600/3 = 1200
Ѳ/2 = 600
We know that for a right angle triangle, 
a = d x 0.866
Here d means pitch circle diameter. So the distance between the two adjacent holes, a = pcd x 0.866.
Example problem:
Question:
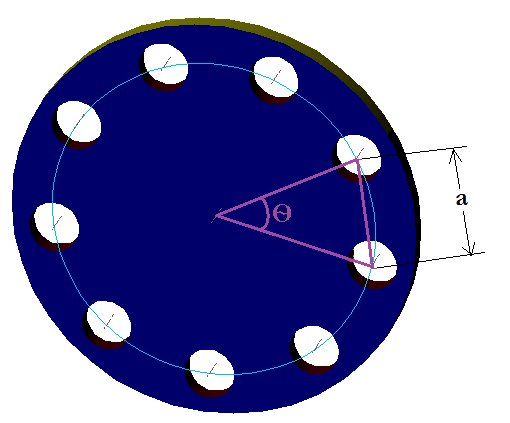
In an SS flange 8 holes to be drilled equally in a circle which has 100 mm diameter. The circle is slightly marked using a tool in the lathe. But it has to be divided into eight using divider. What is the measurement to be set in the divider?
Hint: The circle is called pitch circle and the diameter of the circle is called pitch circle diameter.
Given Data:
Pitch circle diameter, pcd = 100 mm
Solution:
The formula from the article to divide the pitch circle into eight is
a = pcd x 0.3827
a = 100 x 0.3827
a = 38.27 mm
Answer:
The measurement to be set in the divider is 38.27 mm.
Explanation:

The total degree of the circle = 3600
If we form a triangle as shown in the figure,
We could see the adjacent sides of the triangle forms degree Ѳ and if we divide the triangle into two it forms a right angle triangle with Ѳ/2 degree.
Ѳ = 3600/8 = 450
Ѳ/2 = 22.50
We know that for a right angle triangle,

a = d x 0.3827
a = pcd x 0.3827
a = 100 x 0.3827
a = 38.27mm
PCD Division Formula Table:
Here, we can find the pcd division using the formula given in the table.
|
No. of holes in the Pitch Circle |
Diagram |
Formula |
|---|---|---|
|
3 holes |
|
a = pcd x 0.866 |
|
4 holes |
|
a = pcd x 0.7071 |
|
5 holes |
|
a = pcd x 0.5878 |
|
6 holes |
|
a = pcd x 0.5 |
|
7 holes |
|
a = pcd x 0.4339 |
|
8 holes |
|
a = pcd x 0.3827 |
|
9 holes |
|
a = pcd x 0.342 |
|
10 holes |
|
a = pcd x 0.309 |
|
Note: To calculate the division of the PCD, multiply the diameter of the pitch circle and the given factor in the table. If 10 holes to be divided in a 100 mm pitch circle then the division, a = pcd x 0.309 = 100 x 0.309 = 30.90 mm. Here, PCD means Pitch circle diameter and so diameter 100 is taken as PCD.
|
||
Continuation for Four holes to ten holes:
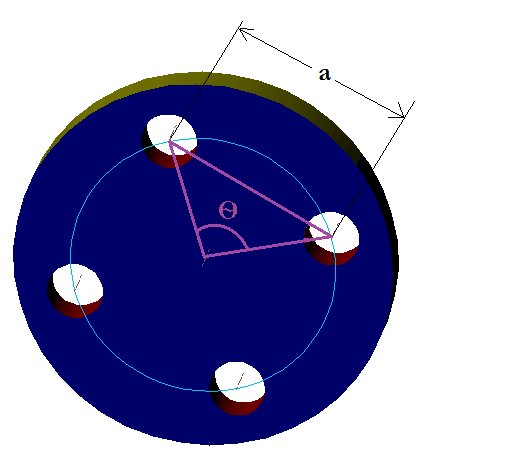
2.For four holes:


The total degree of the circle = 3600
If we form a triangle joining the centre of the circle and the centre of the two adjacent holes as shown in the figure,
We could see the adjacent sides of the triangle forms degree Ѳ and if we divide the triangle into two it forms a right angle triangle with Ѳ/2 degree.
Ѳ = 3600/4 = 900
Ѳ/2 = 450
We know that for a right angle triangle,

a = d x 0.7071
a = pcd x 0.7071
3.For five holes:


The total degree of the circle = 3600
If we form a triangle joining the centre of the circle and the centre of the two adjacent holes as shown in the figure,
We could see the adjacent sides of the triangle forms degree Ѳ and if we divide the triangle into two it forms a right angle triangle with Ѳ/2 degree.
Ѳ = 3600/5 = 720
Ѳ/2 = 360
We know that for a right angle triangle,

a = d x 0.5878
a = pcd x 0.5878
4.For six holes:


The total degree of the circle = 3600
If we form a triangle joining the centre of the circle and the centre of the two adjacent holes as shown in the figure,
We could see the adjacent sides of the triangle forms degree Ѳ and if we divide the triangle into two it forms a right angle triangle with Ѳ/2 degree.
Ѳ = 3600/6 = 600
Ѳ/2 = 300
We know that for a right angle triangle,

a = d x 0.5
a = pcd x 0.5
5.For seven holes:


The total degree of the circle = 3600
If we form a triangle joining the centre of the circle and the centre of the two adjacent holes as shown in the figure,
We could see the adjacent sides of the triangle forms degree Ѳ and if we divide the triangle into two it forms a right angle triangle with Ѳ/2 degree.
Ѳ = 3600/7 = 51.42860
Ѳ/2 = 25.71430
We know that for a right angle triangle,

a = d x 0.4339
a = pcd x 0.4339
6.For eight holes:


The total degree of the circle = 3600
If we form a triangle joining the centre of the circle and the centre of the two adjacent holes as shown in the figure,
We could see the adjacent sides of the triangle forms degree Ѳ and if we divide the triangle into two it forms a right angle triangle with Ѳ/2 degree.
Ѳ = 3600/8 = 450
Ѳ/2 = 22.50
We know that for a right angle triangle,

a = d x 0.3827
a = pcd x 0.3827
7.For nine holes:


The total degree of the circle = 3600
If we form a triangle joining the centre of the circle and the centre of the two adjacent holes as shown in the figure,
We could see the adjacent sides of the triangle forms degree Ѳ and if we divide the triangle into two it forms a right angle triangle with Ѳ/2 degree.
Ѳ = 3600/9 = 40 Ѳ/2 = 200
We know that for a right angle triangle,

a = d x 0.342
a = pcd x 0.342
8.For ten holes:


The total degree of the circle = 3600
If we form a triangle joining the centre of the circle and the centre of the two adjacent holes as shown in the figure,
We could see the adjacent sides of the triangle forms degree Ѳ and if we divide the triangle into two it forms a right angle triangle with Ѳ/2 degree.
Ѳ = 3600/10 = 360
Ѳ/2 = 180
We know that for a right angle triangle,

a = d x 0.309
a = pcd x 0.309
We have given from 3 to 10 holes for your reference. But you can calculate for more than 10 holes using the same procedure.
If you have any doubt please comment below.
What's Your Reaction?